Teoria obwodów, czyli elektrotechnika w pigułce IV

Nie będę skupiał się na wzorach - postaram się w prosty sposób przedstawić złożoność tego zagadnienia - będzie dużo uproszczeń (sam miałem 1,5 roku teorii obwodów i wiele przedmiotów ściśle związanych - zabrakłoby miejsca na napisanie przynajmniej 10% teorii, by była zrozumiała dla wszystkich).

Bez znajomości podstaw teorii obwodów elektryk nie jest w stanie policzyć prostych rzeczy, a o skomplikowanych nie ma już mowy. Podstawy pozwalają na np. wykonanie pewnych obliczeń na systemie elektroenergetycznym - obliczenia rozpływowe (jak moc płynie w liniach), zwarciowe (jak dobrać parametry do dużych prądów) i stabilności (czy generator się rozleci).

Parametry

Podstawą większości obliczeń w elektryce są parametry elementów obwodu (np. w obliczeniach zwarciowych). Trzeba wiedzieć czym one są w teorii i praktyce.
Rezystancja (R) - opór elektryczny czynny. Związana jest z wydzielaniem się ciepła w przewodniku. Jej wartość zależy od wymiarów przewodnika i materiału. W obliczeniach zakłada się, że jest wartością stałą i jest stosunkiem napięcia (U) i prądu (I) - nie zawsze tak jest. Zmiana temperatury wpływa na rezystancję, a w elementach nieliniowych stosunek U/I nie jest zachowany. Ale tym głowy nie warto na początku sobie zaprzątać. Teoretycznie nie zależy od częstotliwości.

Jako ciekawostkę można dodać, że poniższe wzorki służą do obliczenia tego samego (sorki za jakość, ale to część mojego zeszytu):


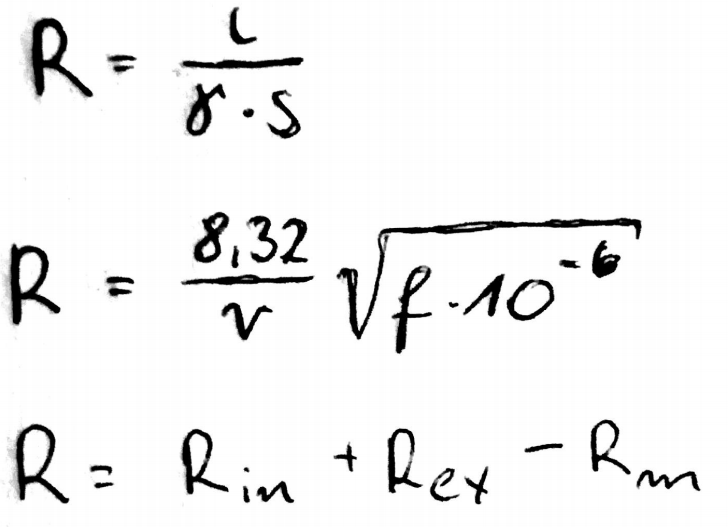
Reaktancja (X) - opór elektryczny bierny. Jej wartość zależy tylko od wymiarów geometrycznych układu (odległość między przewodami roboczymi, ich przekrój). Występuje w obwodach z cewkami i kondensatorami. Poniższe dwa wzorki obliczają to samo (drugi został znacznie uproszczony).


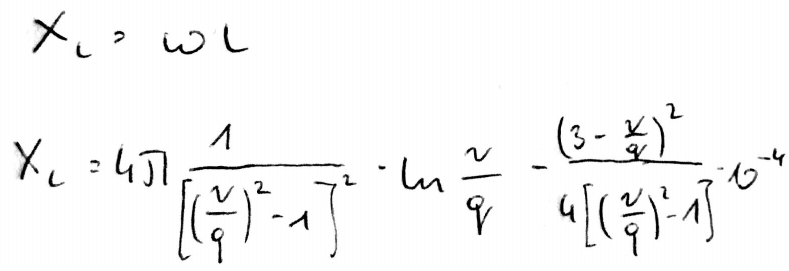
Zmienia się z częstotliwością (im większa częstotliwość, tym większa reaktancja cewki i mniejsza kondensatora). W liniach związana jest z indukcyjnością linii (jakie zdolności ma do wytworzenia pola).

Konduktancja (G) - przewodność elektryczna czynna. Jest odwrotnością rezystancji. W liniach wiąże się z upływnością izolacji (ile prądu „ulatuje” przez izolację).
Susceptancja (B) - przewodność elektryczna bierna. Jest odwrotnością reaktancji. W liniach związana jest z pojemnością doziemna linii (linia i ziemia tworzą kondensator).
Impedancja (Z) - opór elektryczny pozorny. Jest wielkością zespoloną (liczby jako wektory na płaszczyźnie, można wyciągać pierwiastki z liczb ujemnych). Oblicza się jako pierwiastek sumy kwadratów R i X. Po prostu zamieniamy sobie rezystory, cewki i kondensatory w obwodzie na jeden element o takich samych parametrach - składamy dwa wektory do kupy i wychodzi jeden.
Admitancja (Y) - przewodność elektryczna pozorna. Jest odwrotnością Impedancji.

Prawo Ohma

Do czego nam są te parametry? Do prawa Ohma. W prądzie stałym stosunek napięcia do prądu jest rezystancją. W prądzie przemiennym zastępuje go impedancja. Wynika z tego tyle, że przy przepływie prądu przez przewodnik o danej rezystancji odkłada się na nim spadek napięcia. Przy zwiększeniu prądu dwa razy, ten spadek będzie też dwa razy większy.
Dlatego napięcie na końcu linii jest mniejsze od napięcia na początku (nie zawsze!).



Prawa Kirchhoffa

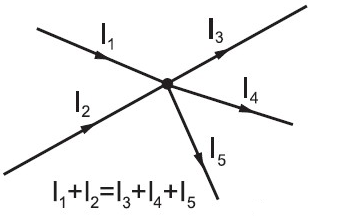
Pewien fizyk stworzył prawa, które dla elektryków są ważniejsze od praw człowieka. Pierwsze prawo mówi, że do węzła (punkt, gdzie łączy się kilka gałęzi obwodu) wpływa taki sam prąd, jak z niego wypływa - czyli mając linię, która się rozdziela na dwie, to tyle co płynie pierwszą, powinno płynąć przez sumę dwóch kolejnych.


Drugie prawo jest prawem napięciowym - mając oczko (obszar zamknięty dookoła obwodem), to spadki napięć na elementach tego oczka w sumie dadzą zero (albo napięcie źródła, jeśli takie jest w tym oczku).
Na podstawie tych 2 praw obliczymy wszystko.



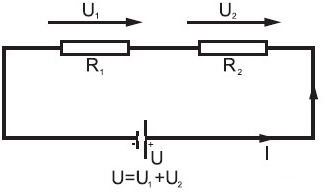
Prąd stały a przemienny

Prąd stały jest w miarę prostym zagadnieniem. Praktycznie wszystkie układy da się rozwiązać stosując prawa Ohma i Kirchhoffa (na te bardziej skomplikowane są metody - oczkowa, superpozycji, węzłowa, Thevenina - ale o nich nie będę pisał).

Gdy jednak wchodzimy w prąd przemienny, rzeczy proste nagle się komplikują. Do rezystancji dochodzi reaktancja i impedancja, zamiast napięcia mamy wartość zespoloną (jako wektor napięcia), skuteczną (odpowiednik prądu stałego, który wydzieli tyle samo ciepła), wartość chwilową i częstotliwość (prąd zmienia się 50x na sek.), wartość średnią, przesunięcie fazowe (sinusoidy napięcia i prądu są przesunięte względem siebie).


Gdyby tego było mało, dochodzą zjawiska przejściowe (stany nieustalone) - przy włączeniu bądź wyłączeniu obwodu dochodzi do gromadzenia energii w kondensatorach i cewkach. Trzeba zwracać uwagę na cewki, które mogą oddziaływać na siebie (pole jednej wpływa na prąd drugiej i wzajemnie). Nagle też pojawiają nam się jakieś moce czynne, bierne i pozorne. Jak się w tym odnaleźć? Zaraz podpowiem.


Moc czynna, bierna i pozorna

Tu zaczyna się zabawa. Moc czynna (P) zamieniana jest na pracę i ciepło, moc bierna już nie. Czym więc ona jest?

Moc bierna (Q) występuje przy prądzie przemiennym. Wiąże się ona z ciągłym przepływem (pulsacją) energii między cewkami/kondensatorami i źródłem oraz ich wzajemnym ładowaniem i rozładowywaniem się. Nie wytwarza ciepła ani pracy jak moc czynna, ale bez niej silnik czy transformator nie będzie działać. Mimo to, gdy przepływa przez linie, to powoduje straty mocy czynnej, więc trzeba ograniczać jej przepływ. Można ją porównać do dziecka z ADHD biegającego od taty w salonie do mamy w kuchni.

Pozorna moc (S) to podobnie jak w przypadku impedancji czy admitancji jest odpowiednikiem złożenia „do kupy” mocy czynnej i biernej (pierwiastek sumy kwadratów).


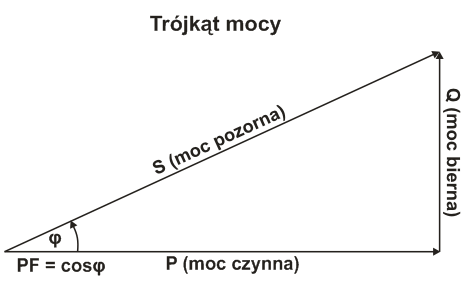
ALE… kolejna zabawa zaczyna się przy prądach i napięciach odkształconych. Okazuje się, że moc czynna i bierna nagle… nie dają nam mocy pozornej. Pojawiają się moce dystorsji (odkształcenia), które mają uzupełnić równanie. Najlepsze, że jest kilka teorii opisujących to zjawisko i każda ma swoją grupę fanów :) Jak tu nie zwariować?


Wartości zespolone, a skuteczne

Do tej części artykułu pewnie już niewiele osób wytrwało. Ci nieliczni (nieelektrycy) zastanawiają się, czy to koniec komplikacji. Otóż nie.

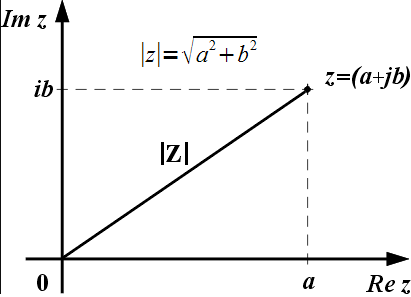
Zaczynając swoją przygodę miałem dość sporo wątpliwości, kiedy można polegać na wartościach skutecznych (modułach), a kiedy trzeba liczyć wartościami zespolonymi. Czym jest ten moduł? Jest to nasz ulubiony pierwiastek sumy kwadratów :-) Pozwala on ocenić wartość danego parametru (jest długością wektora). Skoro mamy już takie wartości, to czemu nie liczyć wszystkiego nimi? Podstawowa zasada - nie dodawaj modułów. Okazuje się, że gdy wektory chce się sumować, ale są względem siebie pod kątem, to dodawanie modułów wprowadza błąd. Dlatego na początek najlepiej przygotować dobry kalkulator, dodawać do siebie liczby zespolone, a potem obliczyć… pierwiastek sumy kwadratów :-)



Obwody prądu trójfazowego

Całe szczęście, gdy ktoś potrafi liczyć obwody prądu przemiennego, to poradzi sobie z tymi trójfazowymi. Gdy zasilanie jest symetryczne (napięcia są co do wartości takie same) i gdy odbiornik jest symetryczny (pobiera na trzech fazach taki sam prąd - co do wartości), to można taki obwód obliczyć jako jednofazowy i będzie super. Gdy jednak coś się stanie z naszym obwodem złego - stracimy jedna fazę, napięcia będą się różnić - no to zaczyna się problem. Można liczyć to jako obwód jednofazowy z różnymi źródłami, pomęczyć się dość mocno. Przy skomplikowanych obwodach to możemy na wieki utknąć w tych obliczeniach. Na ratunek jednak przychodzi największy przyjaciel elektryka - składowe symetryczne (o tym zaraz).



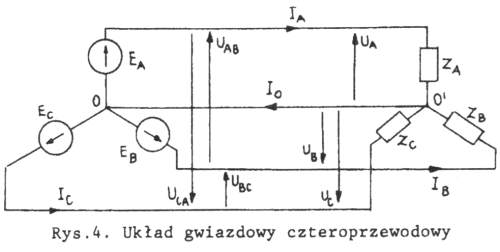
Wyższa szkoła jazdy - składowe symetryczne

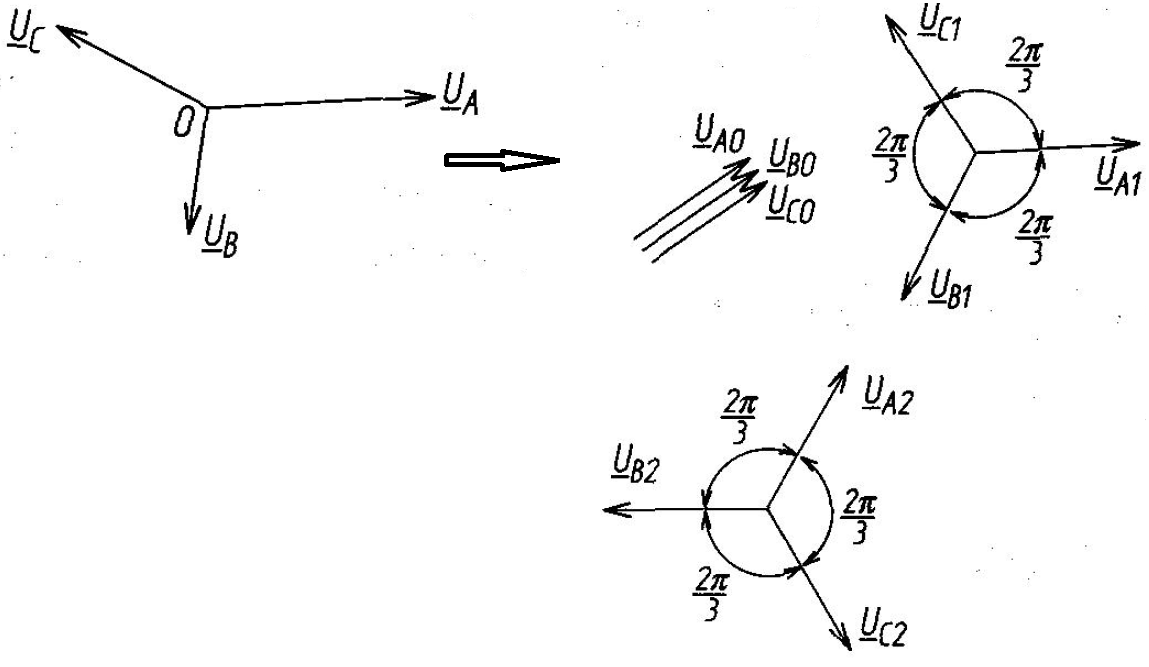
Mówiąc, że jest to największy przyjaciel elektryka przy obliczaniu obwodów trójfazowych, wcale nie przesadzałem. Metoda polega na tym, że mając sobie trzy napięcia lub prądy w układzie trójfazowym i gdy są one „pokrzywione”, czyli występuje jakaś asymetria, to jednym równaniem możemy z takiego układu zrobić… 3 kolejne :-) Tylko że tym razem są one symetryczne.

Pierwsza składowa zgodna - odpowiada za kolejność faz, taką jaka jest w obwodzie. Druga składowa przeciwna - odpowiada za odwrotną kolejność faz. Ostatnia składowa zerowa jest najciekawsza - odpowiada za pojawienie się prądu, który w odbiorniku nie kompensuje się wzajemnie z 3 faz, a sumuje - jedna faza jest powielona 3-krotnie. Detekcja zwarć doziemnych bazuje na tej składowej. To, jakie te składowe mają wartości, pozwala na ocenę zachowania się obwodu. I pozwala w prosty sposób liczyć wszystko, praktycznie jak dla obwodu jednofazowego.



Linia długa - efekty falowe

Gdy powiem wam, że rezystancja zależy od częstotliwości, to pewnie parę osób uznałoby mnie za niedouczonego. Okazuje się, że to prawda. Przy dużych częstotliwościach rezystancja zaczyna zmieniać się z częstotliwością - pojawia się efekt naskórkowości. Prąd lubi płynąć sobie bliżej krawędzi przewodnika - więc przekrój skuteczny maleje, zwiększa się rezystancja. Przy wysokich częstotliwościach mają sens przewodniki rurowe. A to tylko początek.

Wracając do tytułu tego punktu - czym jest linia długa? Jest to linia, której długość jest porównywalna z długością fali, jaka przez niego przepływa. Dla 50 Hz jest to 6000 km - no troszkę dużo. Ale dla wysokich częstotliwości jest to wartość znacznie mniejsza (dla 1 MHz jest to już 300 m). W takich warunkach w liniach może dochodzić do odbijania się takiej fali w węzłach (połączenie linii o różnych impedancja falowych).

Chwila, chwila - a ta impedancja falowa to skąd? Jest to kolejna impedancja - tym razem dla przenoszenia fal w tej linii. Tak jak pisałem, przejście miedzy liniami o różnych impedancjach falowych powoduje wielokrotne odbijanie się takiej fali w linii, częściowego przejścia, zwiększenia i zmniejszenia napięcia - czyli jest niebezpieczne dla izolacji układu.
Skąd takie fale w linii? Odpowiedź jest prosta - przepięcia (np. piorun).



Obwody nieliniowe

No i ciekawostka już na sam koniec. Co zrobić, gdy nie działa nam prawo Ohma? W obwodach nieliniowych dochodzi do takiej sytuacji, że zwiększając prąd dwukrotnie, spadek napięcia na elemencie nie zwiększa się dwukrotnie. Rezystancje modeluje się jako element o zmiennych parametrach (wygląda jak opornica suwakowa) - jego wartość to… równanie. Jakoś trzeba sobie z tym radzić - dobrze, że są na to sposoby :-) Ale nie będę was już tym zamęczał.

Jeśli macie jakieś pytania - proszę pytać. Jeśli forma nie jest odpowiednia (nudne, za długo, za krótko, zbyt/za mało uproszczone) - proszę pisać o tym.

Ostrzegam, że ten artykuł został napisany (tak jak poprzednie) głównie w oparciu o wiedzę i doświadczenie - przed pisaniem nie "uczyłem się" na nowo rzeczy, o których średnio mam pojęcie. Może skutkować to pewnymi błędami (czas robi swoje), zbyt dużymi uproszczeniami, skrótami myślowymi. Jest to jednak moja metoda na zachowanie sprawności umysłu - wymaga większego zastanowienia, przywołania zasobów wiedzy i przypomnienia na podstawie zgromadzonych materiałów. Polecam to wszystkim, którzy sądzą, że już nic nie pamiętają po uczelni :-) No i może więcej osób zainteresuję się tym.